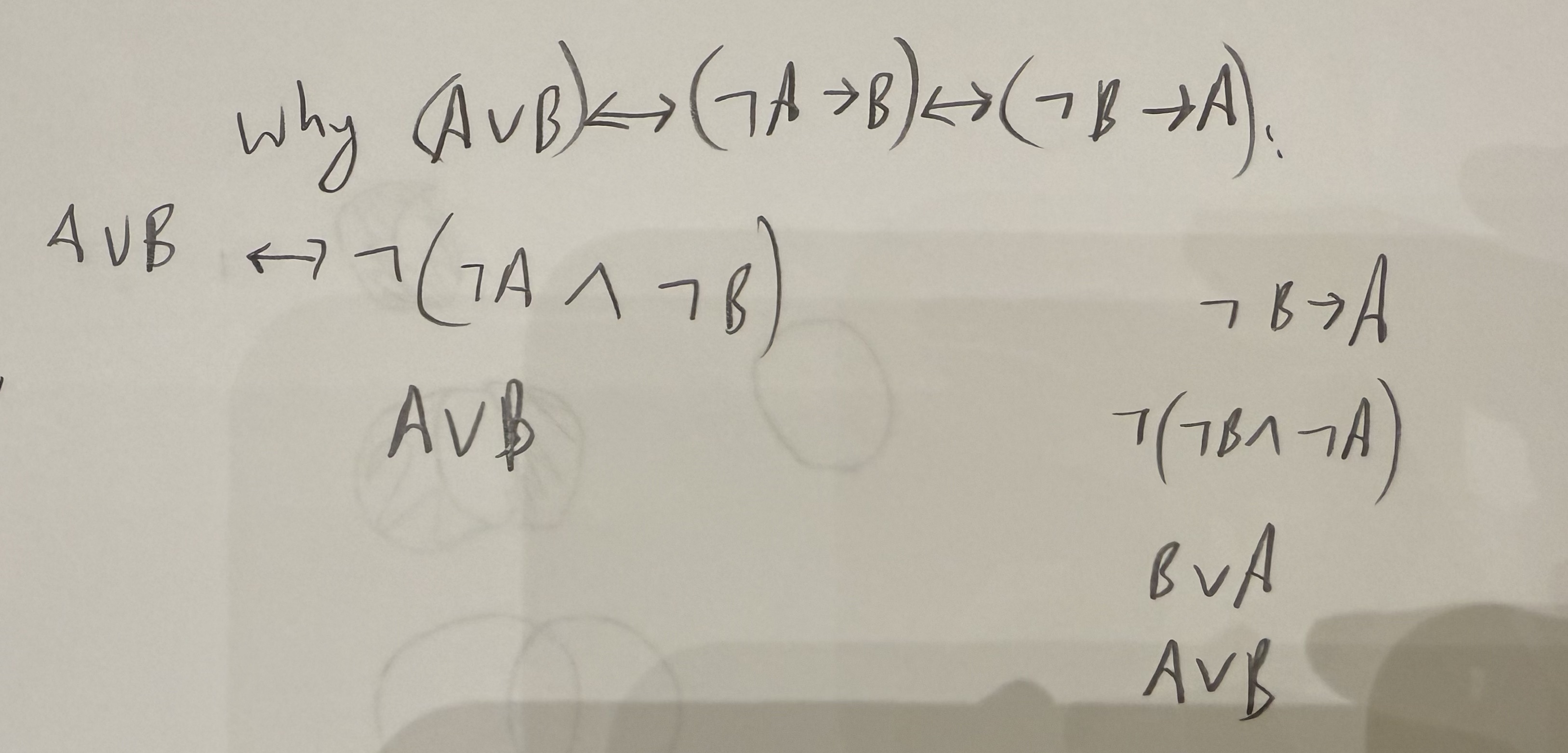Mathematical Foundations of Computing

Computability Theory

• Turing Machine

  • Church–Turing thesis: a Turing machine can simulate every effective form of computation.
    • In other words, no computation can be more effective than a Turing machine.
  • Terminology
    • (accepts, rejects, loops) on a string
    • halts - accepts or rejects (does not loop)
    • does not accept - rejects or loops
  • Decider - will always halt, never loops
    • Definitely accepts $w$ when $w\in L$ and rejects $w$ when $w\not\in L$
    • mn always decides (never loops)
    • R - set of all languages that have a decider for it
  • Recognizer - always accepts $w\in L$. Either rejects or loops on $w$ when $w\not\in L$
    • a Turing machine is a recognizer for $L$ ↔ (it will eventually accept an string $s$ ↔ $s\in L$)
    • mn always recognizes (always accepts when it should)
    • A Turing machine $M$ recognizes (or is a recognizer for) a language $L$ if:
      • If $s \in L$, $M$ eventually accepts $s$
      • If $s \notin L$, $M$ either rejects $s$ or loops forever
    • Formally, $∀w ∈ Σ^*. (w ∈ L ↔ M \text{ accepts } w)$
    • Annoyingly, if you don't know if $w\in L$ and the TM is still running, you can't tell if it loops or just needs more time
    • RE - set of all languages that have a recognizer for it

• Falsifiability -

• Myhill–Nerode Theorem - if $L$ is a language and $S$ is a distinguishing set of $L$ with infinitely many strings then $L$ is nonregular

• Distinguishability - two strings $x$ and $y$ in $\Sigma^\star$ are distinguishable ($x\not\equiv_Ly$) if $xw\in L$ and $yw\not\in L$ (e.g., $x=aa$, $y=aaaa$, and $w=bb$) for some string $w$

  • Formally, $\exists w\in\Sigma^\star.(xw\in L\leftrightarrow yw\not\in L)$
  • Layman: Distinguishable if there is a string w you can add to one that will make it accepting but adding w to the other will make it rejected
  • Distinguishing set - set where each item is distinguishable from each other item

• Constructing NFAs
  • Have the NFA guess the information you want and deterministically check if it is true (guess-and-check technique)
• Regular languages
  • Regular languages are problems that can be solved with finite memory. Nonregular languages correspond to languages that cannot be solved with finite memory, such as $\{a^nb^n|n\in\mathbb N\}$.
  • The following are equivalent: L is a regular language, there exists an NFA or DFA or regex called X such that $\mathscr L(X)=L$ (the language of X is L)

• Kleene closure/star of a language L is L*, which is the set of all strings that can be formed by concatenating any number of strings in L (e.g., L={a,b} means L*={ε, a, b, aa, ab, ba, bb, aaa, ...})
  • Formally, $L^\star=\{w\in\Sigma^\star~|~\exists n\in\mathbb N.w\in L^n~\}$
• Closure properties of languages. If $L_1$ and $L_2$ are regular languages, so are these: $\overline {L_1},\quad L_1\cup L_2,\quad L_1\cap L_2,\quad L_1L_2,\quad L_1^*$
• Language concatenation $L_1L_2$ is the language $\{xy~|~x\in L_1\land y\in L_2\}$
  • xy is the strings x and y concatenated
• Finite automaton - collection of states joined by transitions, has a start state
  • Some states are accepting states. If automaton ends at accepting state, it accepts the input else rejects the input
  • DFA (Deterministic Finite Automaton) - exactly 1 transition at each state for each symbol in $\Sigma$
  • NFA (nondeterministic finite automaton) - each state has 0 or multiple transitions
    • If there is one path that works, NFA accepts
    • Path dies if cannot move at a certain symbol
    • ε-transition - transition that doesn't consume input
    • Works by perfect positive guessing or massive parallelism
    • the term nondeterministic means the automaton has a finite number of choices (possibly 0) to make at a given point
  • Subset construction (AKA powerset construction) is a method for turning an NFA into a DFA
  • A language is regular if there is a DFA D (or NFA) such that $\mathcal L(D)=L$, in which case D recognizes L
• Language - string[] string - character[] alphabet - set<character>
  • (formal) language - set of strings
    • language over $\Sigma$ if is set of strings each over $\Sigma$
    • $\Sigma^*$ is the set of all strings composed from letters in $\Sigma$
  • String
    • empty string - $\varepsilon$
    • String over $\Sigma$ - finite sequence of characters from $\Sigma$ (such as aaaabbaba for $\Sigma=\{a,b\}$)
  • Alphabet $\Sigma$ - set of characters
  • Characters
• Automaton - mathematical model of a computer (abstraction of real computer)
• states linked by transitions

Discrete Math

• Induction
  • P(0) is true - basis/base case
  • P(k) → P(k+1) - inductive step
    • P(k) - inductive hypothesis
  • To prove
• Pigeonhole principle
  • if $n$ items are put into $m$ containers, with $n > m$ , then at least one container must contain more than one item
  • Generalized pigeonhole principle (AKA strong pigeonhole principle)
    • For p pigeons and h holes,
      • some crowded hole will have at least $\lceil {p\over h} \rceil$ pigeons in it
      • not all holes can have more than $\lfloor{p \over h}\rfloor$ pigeons in them
        • some hole will have $\lfloor{p \over h}\rfloor$ or fewer pigeons
• $G^C$ is the graph complement of $G$. All edges are turned into not edges and all not edges are turned into edges in $G^C$.
• subset symbols
  • $\subsetneq$ - proper/strict subset. Cannot be itself.
  • $\subseteq$ - subset or equal
    • includes the improper subset case in which a set is the (improper) subset of itself
  • $\subset$ is ambiguous (could mean $\subseteq$ or $\subsetneq$ in different textbooks)
• Generalized pigeonhole principle
  • For p pigeons and h holes,
    • some hole will have at least $\lceil {p\over h} \rceil$ pigeons in it
    • some hole will have at most $\lfloor{p \over h}\rfloor$ pigeons in it
• The "composition of f and g" is $g\circ f$
• Translating first-order logic to English in a proof:
• Functions
  • domain - function defined for every element of domain
  • codomain - output is always in codomain. Not all els in codomain must have an associated output of the f tho
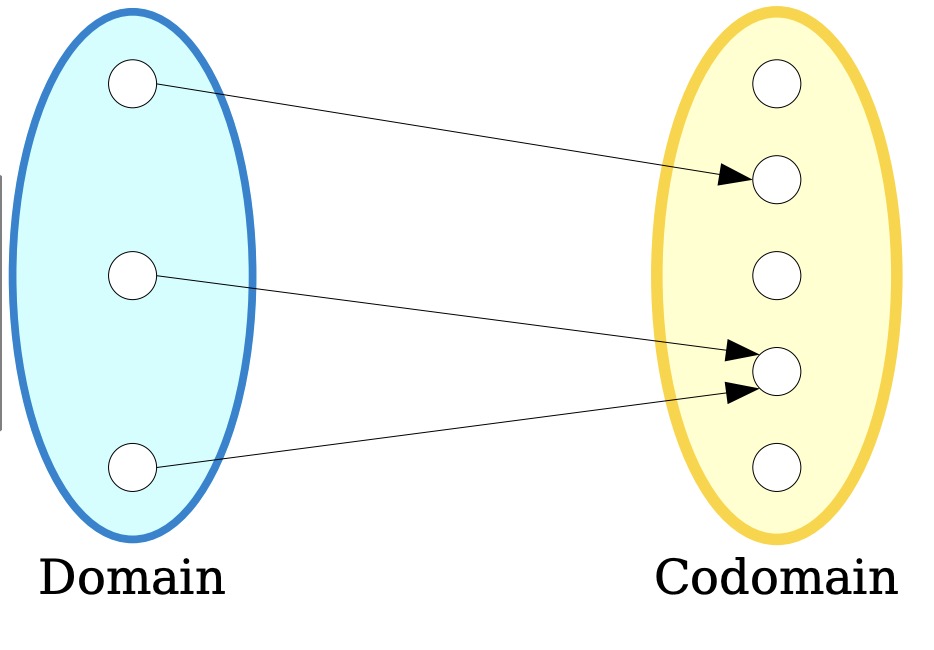
  • $f : A\to B$ means f has domain A and codomain B
  • Involution: a function f is an involution if $\forall a\in A.f(f(a))=a$
    • Layman: apply twice gives same thing back. f is an involution if f(f(x))=x
  • Surjective: $\forall b\in B.\exists a\in A.(f(a)=b)$
    • Layman: all outputs have an input that points to it
  • Injective: $\forall a_1\in A.\forall a_2\in A.(a_1\not=a_2\to f(a_1)\not=f(a_2))$
    • Equivalently $\forall a_1\in A.\forall a_2\in A.(f(a_1)=f(a_2)\to a_1=a_2)$
    • Layman: one-to-one function. No no output maps to two inputs. Every output maps to 1 or 0 inputs.
      • one-to-one function (not every codomain element needs to be used)
      • horizontal line test in y=f(x) tells you if a function is injective
  • Said differently, surjective associates each codomain element with at least one domain element and injective associates each codomain element with at most one domain element
  • bijective - injective and surjective, one-to-one correspondence (ever codomain element used)
  • Function needs to be:
    1. $\forall a\in A.\exists b\in B.(f(a)=b)$ - total
       • Defined on every element in domain, as opposed to partial, which means that f(a) is undefined for some a in the domain
         • Partial - $\exists a\in A.f(a)\text{ is undefined}$
    2. $\forall a_1\in A.\forall a_2\in A.(a_1=a_2\to f(a_1)=f(a_2))$ - deterministic (same input always produces same output)
• Proof explains why theorem is true Disproof explains why claim is false (such as through a counterexample)
• Transformations
  • $\underline{\lnot\forall x.A}$ $\exists x.\lnot A$
  • $\underline{\lnot\exists x.A}$ $\forall x.\lnot A$
  • $\underline{ \lnot (A\land B)} - \text{2 ways}$ $\lnot A\lor \lnot B$ (De Morgan's Law) $A\to\lnot B$
  • $\underline{\lnot(A\lor B)}$ $\lnot A\land \lnot B$ (De Morgan's Law)
  • $\underline{\lnot(A\to B)}$ $A\land\lnot B$
  • $\underline{\lnot(A\leftrightarrow B)}$ $\lnot A\leftrightarrow B$ $A\leftrightarrow\lnot B$
  • Mnemonics
    • "Pushing" $\lnot$ inward and flipping between operators (or vice versa):
      • $\land$ to $\to$
      • $\forall$ to $\exists$
    • De Morgan's Law is like distributing the $\lnot$ and flipping the operator (from $\land$ to $\lor$ or vice versa)
    • When applying $\lnot$ to the biconditional ($\leftrightarrow$) negate either side and keep the operator same
    • $p \to q$ is the same as $\lnot(p \land \lnot q)$
      • only false when p is true and q is false
  • Others
    • $p\to b\to r$ same as $p\land q\to r$
• The Aristotelian Forms
  • All As are Bs: $\forall x.(A(x) \to B(x))$
  • No As are Bs: $\forall x.(A(x)\to \lnot B(x))$
  • Some As are Bs: $\exists x.(A(x) \land B(x))$
  • Some As aren't Bs: $\exists x.(A(x)\land\lnot B(x))$
• First-order logic
  • Terms
    • Functions - object → object Predicate - object → bool
    • Connective - bool(s) → bool
      • conjunction - $\land$ (binary)
      • disjunction - $\lor$
      • implication - $\to$
      • biconditional - $\leftrightarrow$
      • negation - $\lnot$ (unary)
      • truth - $\top$ (nullary)
      • falsity - $\bot$
    • Quantifier - bool → bool
  • Examples
    • = operates on objects, $\leftrightarrow$ operates on predicates
    • Some P is a Q translates to $\exists x.(P(x) \land Q(x))$
    • All Ps are Qs translates to $\forall x.(P(x)\to Q(x))$
  • Try to pair $\exists$ with $\land$ and $\forall$ with $\to$
• Precedence (highest to lowest)
  • $\lnot$
  • $\forall$ and $\exists$
  • $\land$ (and before or)
  • $\lor$
  • $\to$
    • $\to$ is right-associative so $a\to b\to c$ is $a \to (b\to c)$. Most operators like $\land$ are left-associative.
  • $\leftrightarrow$
• Propositional logic
  • Propositional variable
  • Propositional connectives
• Universal statement - for all x, some [property] holds for x (mn works on x universally)
• Existential statement - there is some x where [property] holds for x (mn some x exists for it to work)
• Proof types
  • Implication: If antecedent, then consequent.
    • Assume step: assume the antecedent is true
    • Want-to-show steps
    • demonstrate that the consequent is true
    • Reiterate what you wanted to show$\square$

Derivations

Myhill-Nerode Theorem

Myhill–Nerode Theorem: if L is a language and S is a distinguishing set for $L$ that contains infinitely many strings then $L$ is nonregular. Proof: Pick an arbitrary language $L$ and a distinguishing set for $L$ that contains infinitely many strings. We want to show that $L$ is nonregular. To do so, assume for the sake of contradiction that $L$ is regular. This means that there exists a DFA D such that $\mathscr L(D)=L$. Let $k$ be the number of states in $D$. Pick $k+1$ strings from $S$. Since we picked $k+1$ strings and there are $k$ states in the DFA, there must be one state with $2$ strings $s_m$ and $s_n$. Since $S$ is a distinguishing set, $s_m$ and $s_n$ cannot map to the same state of a DFA. We have reached a contradiction, so our earlier assumption must have been false. Therefore, $L$ is nonregular.

$p\to q\equiv\lnot p\vee q$

De Morgan's Laws

$(A\lor B)\leftrightarrow(\lnot A\to B)\leftrightarrow(\lnot B\to A)$