Multivariable Calculus

I learned about multivariable calculus in spring quarter of freshman year in Math 52: Integral Calculus of Several Variables.

Link to Openstax textbook

• Spherical coordinates

  • Colatitude $\phi$
  • Azimuthal angle $\theta$

• LatLng (except for GeoJSON where it is LngLat)

  • Latitude $\phi$
  • Longitude $\lambda$

• Co as in complementary (as in 90°-X) as in complementary angle (add up to 90°)

  • cos - complement of sine
    • cos(X)=sin(90°-X)

• 2D tangential form: Green's theorem $\oint_C\vec F\cdot d\vec r=\iint_D (\operatorname{curl}\vec F) \cdot d\vec A=\iint_D Q_x-P_y~ dA$

• 2D flux form: Green's theorem $\oint_C \vec F\cdot \hat nds=\iint_D \operatorname{div}\vec F dA$

• 3D tangential form: Stokes' theorem $\oint_C\vec F\cdot d\vec r=\iint_S (\operatorname{curl}\vec F) \cdot d\vec A$

• 3D flux form: Divergence theorem $\iint_{\partial E} \vec F\cdot \hat nds=\iiint_E \operatorname{div}\vec F dV$

• Conservative vector field properties

  • Cross-partial property: $P_y=Q_x$ etc.
  • Work done = 0
  • Line integral is path-independent
  • Fundamental Theorem of Line Integrals applies

• Source-free vector fields

  • Flux and flux are 0

• Integrals

  • Scalar line integral $\int_C fds=\int_{t=a}^bf(\vec r(t))||\vec r'(t)||dt$
  • Vector line integral $\int_C\vec F\cdot \underbrace{\hat T ds}_{d\vec r}=$
  • Surface integrals

• Regions

  • Open vs. closed
  • Simple $\circ$ vs. not simple $\infty$
  • Simply connected - no holes
    • Needed for a conservative vector field test

• $\vec r = \langle x', y'\rangle$ → $\vec n = \langle y', -x'\rangle$ or $\langle-y',x'\rangle$

• Positively oriented curve

  • When walking along a curve, the surface should be to your left if your head points in the $\hat N$ direction for it to be positive orientation.
  • This means the curve is traversed in the counterclockwise direction
  • Integrating over a positive orientation gives outward flux. " over negative orientation gives inward flux

Old reference sheet

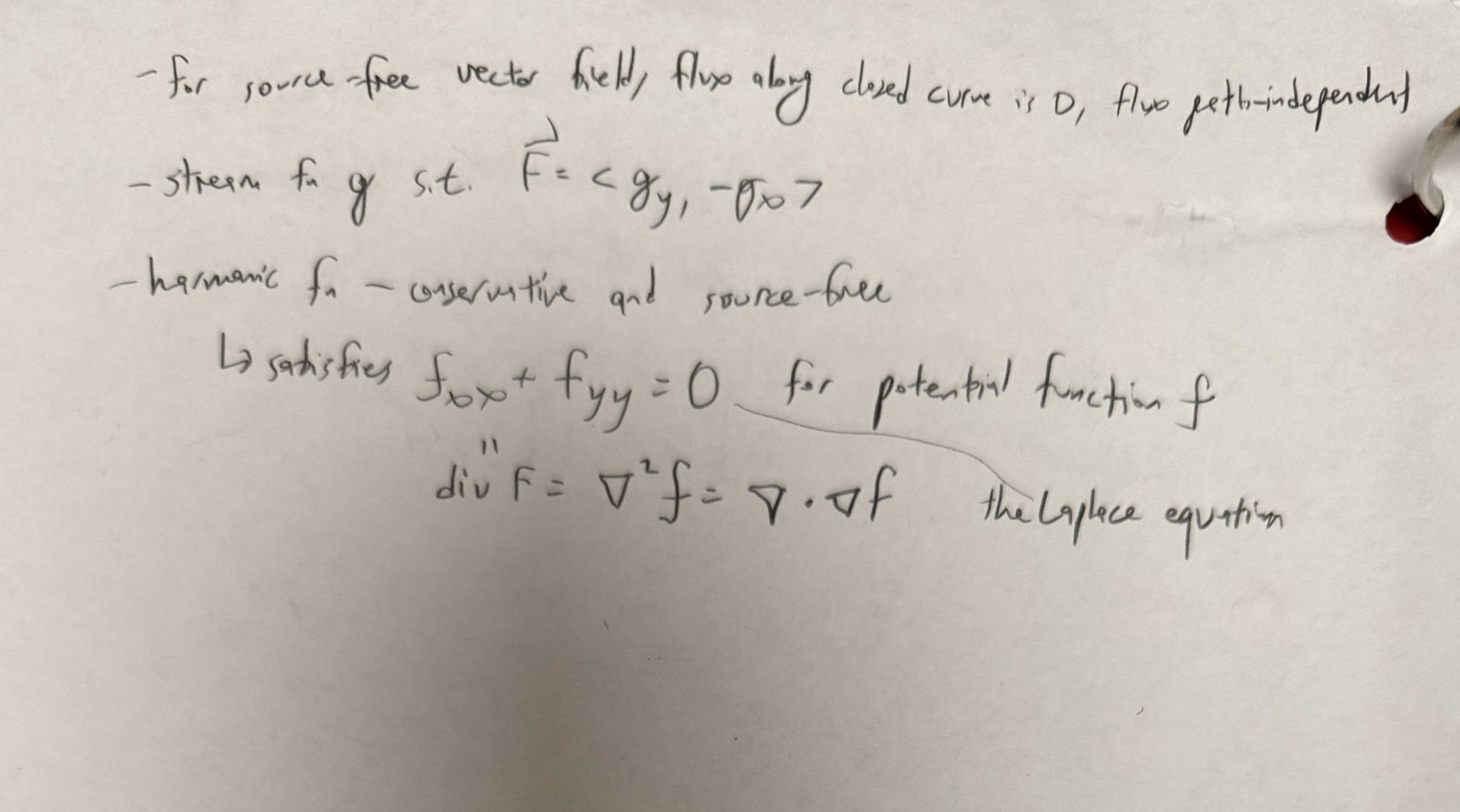
• Iterated integral - method of evaluating nested integrals by doing inner integrals each w.r.t. 1 variable treating the other variables as constants

First Principles Derivations

Why use $r$ in cylindrical coordinate integrals and $\rho^2sin(\phi)$ in spherical coordinates?